零知识证明（ZKP）和多方计算（MPC）都属于隐私保护密码学范畴，但它们的用途却截然不同。ZKP 允许参与方在不泄露秘密的情况下证明其知晓该秘密（例如，在不泄露任何敏感凭证的情况下证明身份），即使在多方参与的情况下也是如此。而 MPC 则允许多方在不暴露输入数据的情况下，共同计算基于其私有输入的函数。

多方计算的关键突破在于，各方可以在不向任何人透露数据的情况下协作进行计算。

历史

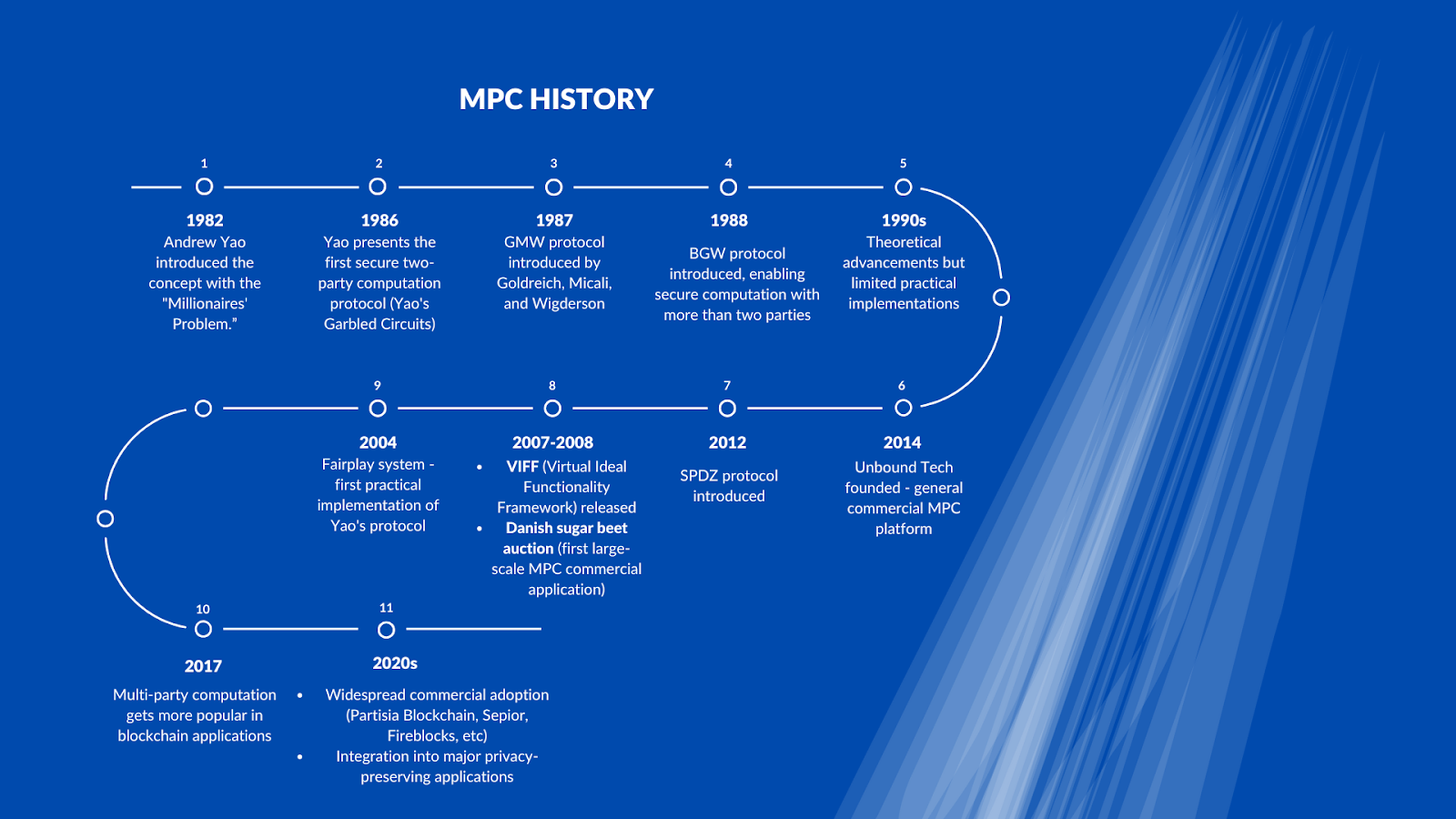
多方计算（MPC）作为密码学中的一个理论概念，于 20 世纪 80 年代出现，但其实际应用却历经数十年才得以实现。以下是其发展历程中的关键里程碑——从姚氏混淆电路等早期协议到现代区块链集成。该时间线突显了 MPC 如何从学术研究过渡到现实世界的隐私解决方案。

时间轴展示了多方计算 (MPC) 的历史和关键里程碑，从 1982 年 Andrew Yao 提出的百万富翁问题到 2020 年代的广泛商业应用。

核心概念

隐私保护

多方计算通过数学保证来确保输入隐私。该协议在数学上防止参与者获知其他参与者的输入，同时仍然允许对这些输入进行计算。

分布式信任

没有哪个单一方掌握所有数据或控制计算过程。多方计算的安全性源于信任在多个参与者之间的分散，使其能够抵御单个参与者的攻击。

那么，这一切为什么如此重要呢？让我们来探讨一下为什么多方计算对当今的隐私需求至关重要。

MPC的重要性

模型计算（MPC）解决了数据隐私领域的一个特定问题：如何在不泄露敏感数据的情况下进行计算。这之所以重要，原因有以下几点：

1.数据隐私法：组织在分析数据时必须遵守《通用数据保护条例》( GDPR ) 和《加州消费者隐私法案》( CCPA ) 等法规。2 .跨组织协作：公司可以在不共享机密信息的情况下开展合作。3 .单点故障：传统的将数据收集和集中存储在单一位置的系统会带来安全风险。4 .信任最小化：多方计算 (MPC) 消除了对单一可信第三方的依赖。例如，组织可以在不共享原始数据的情况下进行协作，加密系统（例如零知识证明 (ZKP) 可信设置）可以在没有中央机构的情况下安全地生成公共参数。

但MPC是如何抵御潜在威胁的呢？让我们来看看它背后的安全模型。

理解MPC安全模型

在模型预测计算（MPC）中，什么是对手？

在多方计算（MPC）协议中，“攻击者”指的是试图破坏协议安全性的参与者（或参与者群体）。攻击者是系统中的恶意行为者。他们可能是：

外部攻击者试图获取私人信息
参与实验方案但不遵守规则的人员
受损方（例如被黑客入侵的服务器）

因此，MPC协议的设计围绕着两个基本问题展开：

对抗性设置：在协议的安全保证失效之前，最多可以有多少参与者被腐败？（注：在学术论文中通常简称为“设置”）。例如：一个为不诚实多数设置（如下所述）设计的协议，即使5个参与者中有4个腐败，也能在数学上保证其安全性。
对抗行为：各方可以使用哪些策略来攻击系统？例如：被动观察者可能能够推断出私人数据，而主动攻击者可能伪造输入或串通攻击。

这些问题定义了该协议对串谋的抵抗力（例如，多个腐败方秘密共享数据以侵犯隐私）以及其处理对抗行为（如窃听（拦截消息以推断私人输入）或破坏（故意扰乱计算））的能力。

安全模型描述了这些攻击者可能采取的行动以及协议如何防御这些行动。多方计算中的一些主要安全模型包括：

半诚实安全模型（被动/诚实但好奇）

它的含义：

半诚实安全模型假设攻击者遵循协议规则，但试图从交换的消息中推断出私密信息。能够抵御半诚实攻击者的协议（称为半诚实安全协议）确保即使攻击者被动地分析协议交互，也无法推断出私密输入。

工作原理：

半诚实安全协议使用诸如混淆电路和秘密共享方案（稍后讨论）之类的密码学原语，以确保任何一方都无法在未经合作（例如，获得足够的秘密份额）的情况下重构私有数据。

使用案例：

银行利用多方计算进行欺诈检测：半诚实安全机制允许多家银行协作分析交易数据并识别欺诈模式，而无需泄露客户记录。半诚实协议在抵御被动攻击者的同时，还能保持处理大规模数据集所需的计算效率。
医学研究合作：半诚实协议允许医院在保护患者隐私的同时联合分析患者基因组。通过最大限度地减少计算开销，这些协议对于基因组研究等数据密集型任务仍然切实可行。

半诚实安全机制的优势：

效率：通常比恶意安全协议需要更少的加密验证步骤（例如，无需零知识证明或选择性验证）。
更低的开销：与主动对抗模型相比，计算成本更低。
可扩展性：非常适合鼓励参与者合作的应用场景（例如，互惠互利的分析）。

恶意（主动）安全模型

它的含义：

恶意安全模型假设攻击者可以任意偏离协议：发送虚假输入、篡改计算或提前中止以破坏结果。而恶意安全协议则保证即使部分参与方作弊，也能确保隐私性和正确性，从而保证输出有效且输入保密。

工作原理：

这种恶意安全协议包含额外的加密验证步骤（例如，零知识证明、选择性验证、经过认证的秘密共享消息认证码），能够从数学上检测并防止作弊。它强制参与方在每个步骤中证明他们正确地遵循了协议，从而保证了输入隐私和计算完整性，即使面对主动攻击者也能有效防御。

使用案例：

投票系统：恶意安全措施确保任何一方都无法提交无效选票（例如，投票给不存在的候选人）或操纵计票结果。例如，零知识证明可以证明选票有效（例如，投给已登记的候选人），而无需泄露个人选择。
加密货币：阈值签名需要恶意安全措施来防止敌对势力篡改密钥生成或窃取资金。检查机制确保私钥永远不会在单一位置被重构。

恶意安全防护的优势：

更强大的安全性：即使协议遭到破坏，隐私性和正确性也能得到保证。
威慑：作弊行为要么被检测到（例如，如果检测到无效的零知识证明，诚实参与方将中止协议），要么在密码学上变得不可能。
高风险适用性：这对于金融结算等应用至关重要，因为错误或泄露会造成严重后果。

其他安全模型，如隐蔽安全，在半诚实安全和恶意安全之间提供了一种中间立场，但这两种是应用最广泛的。

这些安全模型定义了协议如何应对攻击者。让我们来看看决定其实现方式的设置：

MPC设置

不诚实的大多数：

即使只有一个参与者诚实，安全保障依然有效；在五方系统中，即使四方都存在腐败行为，协议仍然是安全的。
这是最保守的安全假设（与诚实的大多数相比），因为它假定大多数参与者都是恶意的。
被SPDZ等协议使用。
由于需要额外的安全措施，不诚实多数协议往往具有更高的计算和通信开销。

诚实的大多数人：

当大多数参与者诚实时，安全保障就能成立；在一个七方系统中，至少需要四方诚实。
BGW协议是一个特例，它需要更多诚实的参与方：为了防止恶意行为，只有不到三分之一的参与方可以被篡改（例如，在一个7方系统中，至少需要5个诚实的参与方）。
与不诚实的大多数人相比，通常能实现更高的效率和更低的沟通复杂性。

基于阈值：

安全性取决于一个阈值（例如，在四方体系中，50%的参与方必须诚实）。
在安全性和效率之间实现了灵活的权衡。

常用的MPC协议

BGW：BGW（Ben-Or、Goldwasser 和 Wigderson）协议于 1988 年提出，是多方计算的基础。它是一种安全的 MPC 协议，允许一组参与者在保持输入私密性的同时共同计算一个函数。它利用密码学技术扩展了 Shamir 的秘密共享（详见下文），从而实现了对私密输入的安全多方计算。BGW 能够抵御半诚实攻击者（如果少于一半的参与者被篡改）和恶意攻击者（如果少于三分之一的参与者被篡改）。
GMW：GMW（Goldreich、Micali 和 Wigderson）协议于 1987 年提出，是一种经典的 MPC 协议，它使用布尔电路表示法。在计算函数时，它将计算分解为逻辑运算（例如 AND、OR、NOT 门），并逐步处理加密数据。它主要针对遵循协议但试图从接收到的消息中获取额外信息的半诚实攻击者。GMW 协议采用诸如不经意传输等技术，以确保每一方仅能从计算中获取其应该获取的信息。
SPDZ：SPDZ（Smart、Pastro、Damgård 和 Zakarias）协议于 2012 年开发，代表了实用多方计算 (MPC) 领域的一项重大进步。SPDZ 使用加性秘密共享（将秘密分割成和等于原始秘密的随机数），并结合基于消息认证码 (MAC) 的校验（使用加密标签确保数据完整性）来确认参与者正确遵循协议。SPDZ 需要一个预处理阶段（预先准备加密材料），并在在线计算阶段（实时执行）实现高性能。它能够抵御恶意攻击者，这意味着即使参与者试图作弊，它仍然安全。

现在，让我们来探讨一下秘密共享如何实现安全计算。

多方计算中的秘密共享

秘密共享允许将一个秘密分成多个部分，称为“份额”，其中：

每位参与者均获得一份份额。
个股并不能揭示这个秘密。
合并足够多的股份就能重构秘密

在阈值秘密共享方案中：

n：秘密被分割成的份额（部分）总数（例如，5）。
t：阈值——重构秘密所需的最小份额数（例如，3）

举个实际例子，请看下面沙米尔分享的秘密。

常见的秘密共享方案：

1.沙米尔的秘密分享

使用有限域上的多项式将秘密分割成若干份。重构过程采用拉格朗日插值法：一定数量的份额可以唯一确定多项式（从而确定秘密）。份额过少则无法揭示任何内容——类似于需要足够的点来定义一条曲线。
灵活的阈值方案：可以使用任意t 个份额（ n 个份额中的t 个）重构秘密，其中多项式的次数为t-1 ，如果可用份额少于t个，则可确保安全性。

例如，在五分之三的评分方案中：

这个秘密分为五份。
任意三份股份都能重构秘密
两股或更少的股票说明不了什么

这就像拼图游戏：你需要一定数量的碎片（“阈值”）才能解开谜题，但单个碎片本身毫无用处。

2.加性秘密共享

将秘密分割成若干随机份额，每个份额的总和等于秘密本身。
重建需要所有份额（如果分成n份，则阈值t等于n）。
用于SPDZ等协议中
与非线性计算相比，它在线性计算（例如加法、求平均值）方面效率更高。

例如：如果秘密数字是 10，则份额可以是 3、5 和 2（3 + 5 + 2 = 10）。必须将所有份额组合起来才能恢复秘密数字。

区块链中的MPC钱包

与存储单个私钥的传统加密货币钱包不同，MPC钱包将密钥生成和签名过程分散到多个独立方。当用户签署交易时，这些参与方会使用加密协议协同工作来生成签名，而无需访问完整的私钥。

这种方法消除了传统钱包中存在的单点故障。私钥不再集中存储在一个位置，因此不存在被盗或丢失的风险。即使某个设备遭到入侵，资金仍然安全，因为攻击者必须同时入侵多个设备。此外，这种安全模型还允许用户添加或移除设备、设置多重授权等，从而实现更灵活的密钥管理。

MPC钱包的示例包括：

ZenGo：一款无需密钥的加密钱包，采用多方计算进行私钥管理。
Fireblocks：一个采用多方支付（MPC）技术的企业级数字资产平台，为Revolut等机构提供数字资产安全保障。

MPC钱包中的阈值签名

MPC钱包使用阈值签名，其中：

私钥被分成若干份。
必须达到规定的股份数量（门槛）才能签署协议。
该签名在数学上与普通签名完全相同。
验证者无法判断它是否是使用 MPC 创建的。

例如：在三方二合一的门槛机制中，必须有两方合作才能签署——单方不能签署。

多方计算与多重签名钱包

多重签名钱包需要多个私钥；每个参与方都持有自己的完整密钥并独立签名。相比之下，MPC钱包使用秘密共享技术将单个私钥拆分成多个份额。任何参与方都不持有完整的密钥，必须协作才能生成单个签名。最终生成的是一个标准的数字签名，其功能与区块链上的任何其他签名相同。

既然我们已经了解了MPC钱包的工作原理，接下来让我们探讨一下它们更广泛的应用——包括现在和未来的应用。

MPC用例

数字资产托管

MPC 为区块链钱包中的加密货币提供安全的密钥管理：

私钥分散在多个参与方之间。
任何一方都无法单独访问或使用密钥。
交易需要协作
如果一方遭到入侵，攻击者无法获取完整密钥，从而保全资产。

保护隐私的分析

MPC使组织能够在不暴露单个输入数据的情况下，从共享数据中获取洞察。例如：

波士顿女性劳动力委员会：与多所大学合作，利用多方薪酬计算（MPC）分析性别薪酬差距，并对个人薪资数据保密。
丹麦甜菜拍卖（2008 年）：第一个大规模商业 MPC 应用，农民在不透露出价的情况下计算公平价格。

保护隐私的机器学习

MPC 无需共享原始数据即可实现协同 AI 训练：

Meta（Facebook）： Meta 的研究团队正在探索MPC 框架，以便在去中心化数据集上训练机器学习模型，同时保护用户隐私。

零知识证明可信设置仪式

MPC 为加密系统（例如，ZKP 可信设置）生成安全参数，确保任何一方都无法获知敏感参数：

Zcash Sapling 仪式：使用 MPC 生成零知识证明的公共参数，防止任何单个参与者破坏系统。

MPC的未来

多方计算的核心优势在于能够在不泄露数据的情况下实现协作，这可以满足一些需要保密领域的复杂需求。例如：

医疗保健：医院可以在不共享病历的情况下，开展跨机构研究（例如癌症研究）和基因隐私保护方面的合作。
金融：银行可以联合进行反洗钱交易筛查和信用评估，而无需透露客户详细信息。
供应链：企业可以在保护商业秘密的同时，对全球供应商进行审核。

结论

多方计算从20世纪80年代的理论概念发展成为如今解决实际隐私挑战的实用技术。它能够在不泄露隐私的情况下处理敏感数据，为各行各业开辟了新的可能性，从帮助医院开展医学研究合作到实现更安全的加密货币钱包，无所不包。

虽然多方计算（MPC）并非解决所有隐私问题的万能方案，但它确实能够让多方在不直接共享数据的情况下进行协作。随着隐私问题日益突出，监管也日趋严格，MPC在实现安全协作方面的作用可能会变得更加关键。

原文：https://www.cyfrin.io/blog/multi-party-computation-secure-private-collaboration

免责声明：本文为c2e Labs的第三方内容，仅供信息分享与传播之目的，不代表我们的立场或观点且不构成任何投资及应用建议。版权归原作者或来源方所有，如内容或素材有所争议请和我们取得联系。

收藏赞（0）

我来评论

登录后回复

yes

第 8 位会员

注册于