我们的目标是根据某一细分市场的实际储量推导出常数乘积公式，该实际储量由下式给出：
%5Cleft%20(%20%7B%7By%7D_%7Br%7D%2BL%5Csqrt%20%7BPl%7D%7D%20%5Cright%20)%5Cleft%20(%20%7B%7D%20%5Cright%20))
并由此恢复上一章中获得的一些公式。
本章为选读章节。与前几章相比，本章并未引入任何全新的概念，而是从不同的角度探讨了如何从价格和流动性推导出实际储备。您可以跳过本章，而不会影响本书其他部分的阅读。
Uniswap 是一个恒定乘积自动做市商。在 Uniswap v2 中，如果我们忽略手续费，资金池中的掉期交易遵循恒定乘积的规则。在公式中 xy=k 保持不变，x 和 y 代表资金池中代币 X 和 Y 的储备。从这个意义上讲，可以说公式 xy=k 定义池中交换的行为。
Uniswap v3 也是一个恒定乘积 AMM，主要区别在于其资金池并非具有恒定的流动性，而是由多个曲线段组成，每个曲线段都具有一定的流动性L。
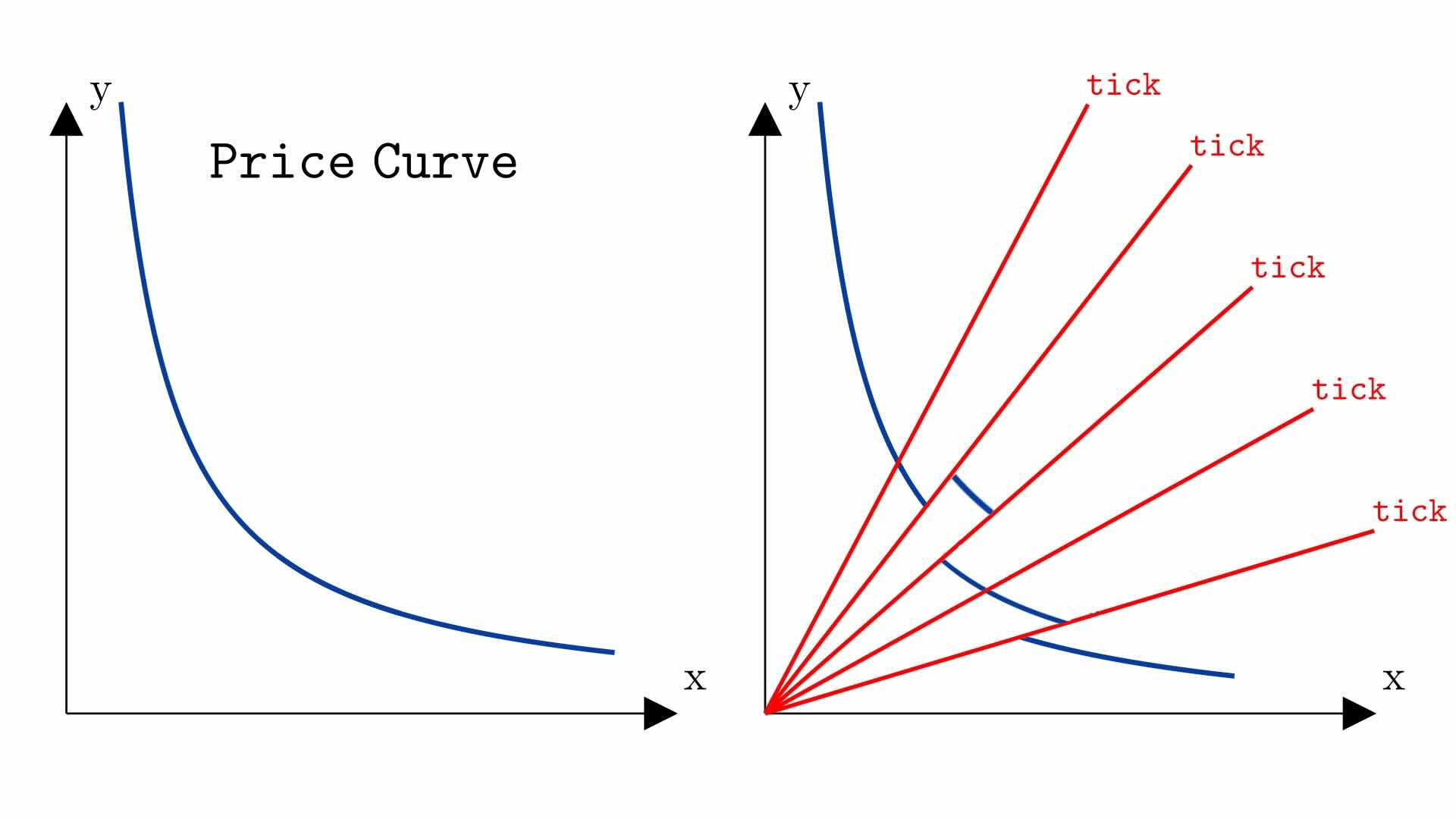
在每个交易段中，互换交易遵循与 Uniswap v2 相同的行为，并且不考虑手续费，必须保持价值不变。L 公式中的常数
只要交换不跨越段的边界。
因此，支配某一板块互换的公式仍然有效。然而与 Uniswap v2 不同的是，x 和 y 不是该段的实际储备，而是其虚拟储备，即如果该段延伸到无限曲线，它将拥有的储备（参见关于实际储备和虚拟储备的章节）。
人们可能会问，常数乘积公式是否成立？ 对于某个板块而言，可以用该板块的实际储备而非虚拟储备来表示。答案是肯定的。事实上，这个公式可以在 Uniswap v3 白皮书的第 2 页找到，如下所示（此处，x 和 y 表示实际储备，我们将其表示为 
和 
（按我们的符号表示）。这与引言中所示的公式相同。
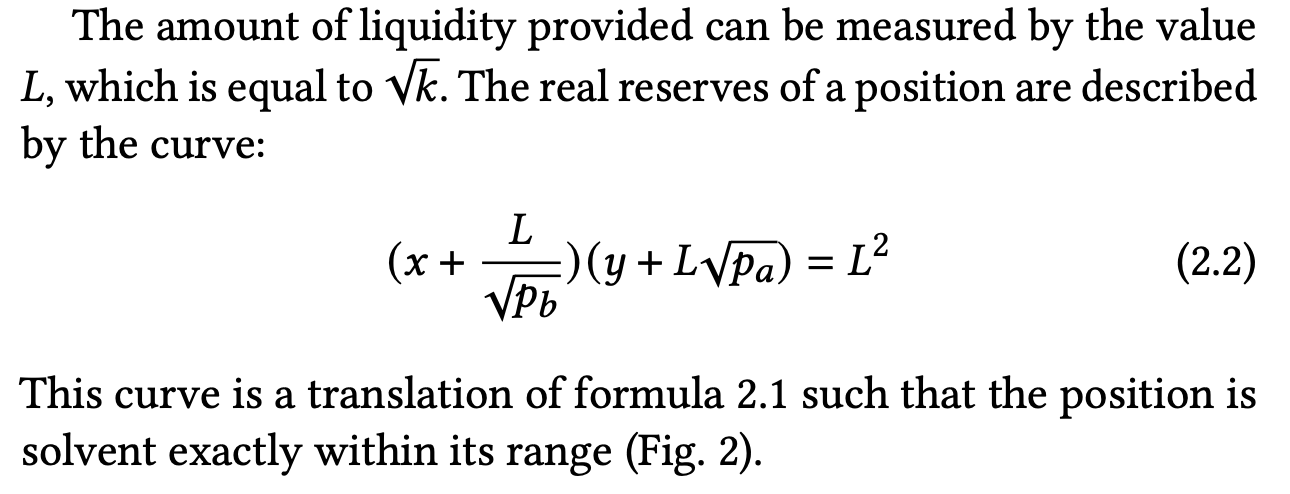
上述公式建立了流动性、分部边界和实际储备之间的关系。在我们的符号体系中，该公式应写成：
在这里 
是最低报价时的价格。
是最高价位，L是流动性。
对于特定细分市场，这些数值是固定的，而实际储备金则会变化。这与 Uniswap v2 类似，其流动性也存在差异。k 已固定，k=xy 以及储备 x 和 y 可能会发生变化。在这两种情况下，公式都限制了可能的储备值——如果一种代币的储备增加，另一种代币的储备就必须减少，以保持流动性不变。
下面的交互式工具可以更直观地展示这个概念。您可以选择上限价、下限价、板块流动性和当前价格。随着价格的变动，实际储备也会随之变化。
和 改变，但要以一种能改变流动性的方式进行。L 保持不变。换句话说，实际储备金与价格之间的比例并非任意设定，而是完全由流动性和价格变动边界决定。
v2 和 v3 的一个主要区别在于，在 v3 中，即使其中一个储备金降至零，另一个储备金也不会趋于无穷大。通常情况下，某个代币的实际储备金会在一个阶段内耗尽，此时价格会进入下一个阶段。
值得注意的是，恒定乘积公式在代码库中并未出现。在 Uniswap v2 中，协议可以简单地在互换交易中强制执行恒定乘积公式。然而，在 v3 中，情况则更为复杂，因为价格在互换交易过程中可能会经过多个阶段。
尽管如此，我们仍然可以利用常数乘积公式推导出实际储备与分段边界、流动性和当前价格之间的表达式。我们在前一章已经通过其他方法推导出了这些公式，因此本章内容为可选内容。
不过，如果读者想要了解恒定乘积公式的由来以及如何利用它来计算一个板块的实际储量，那么这就是本章的目的，我们邀请您继续阅读。
分段的常数乘积公式与 Uniswap v2 中的相同，
但现在 x 和 y 是虚拟储备。
如果我们找到将虚拟储量与实际储量联系起来的方法，就可以推导出实际储量的常数乘积公式。
请看下图，其中 是最低价位的价格，是最高价位。
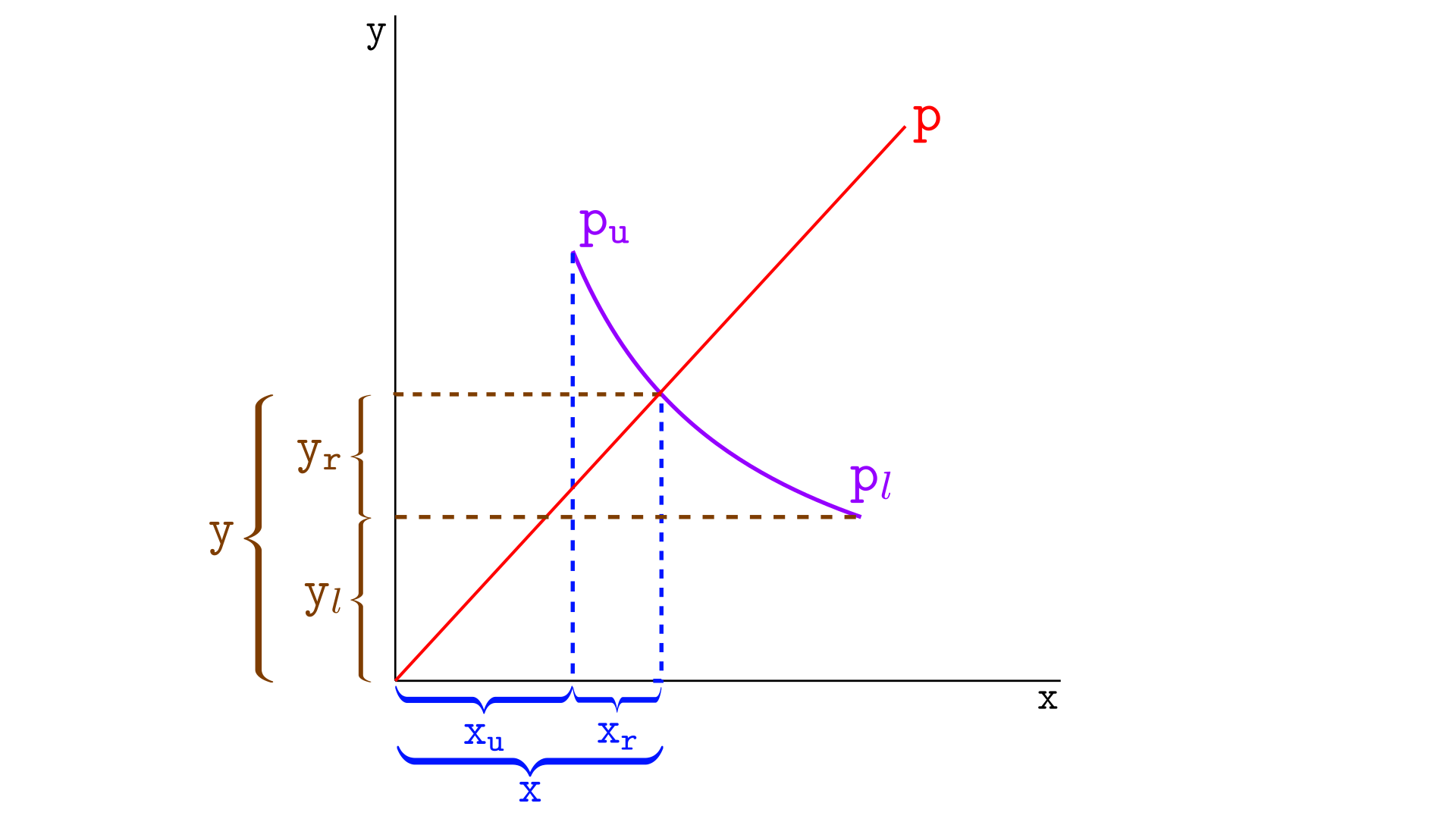
上图中，我们有
(x,y)是当前价格的虚拟储备，
在 阈，
Y 中的虚拟储备是多少？如果该段曲线是无限长的曲线，则该段曲线所包含的代币数量 Y 。然而，我们更感兴趣的是从几何角度来看，比从解释角度来看要好得多。
在阈， 
X 中的虚拟储备是多少？
)
是该领域的真正储备。
虚拟储备与实际储备之间的关系可表示为：
我们可以利用这些关系 替换 x 和 y 要得到
(%7By%7D_%7Bl%7D%2B%7By%7D_%7Br%7D))
在一个片段中， 和 交易过程中可能会有所变化，但是 和 仅取决于线段边界，因此对于该线段而言它们是常数。因此，如果我们能够获得 和 即找到了我们所需的公式。
具有流动性的细分市场的恒定乘积公式L较低的刻度线 以及一个上勾
由下式给出
当 和 为多少时，X 和 Y 代币的实际储备是多少？
原文：https://rareskills.io/post/uniswap-v3-constant-product
免责声明：本文为c2e Labs的第三方内容，仅供信息分享与传播之目的，不代表我们的立场或观点且不构成任何投资及应用建议。版权归原作者或来源方所有，如内容或素材有所争议请和我们取得联系。
